مقدمه
در طراحی و بهینهسازی سیستمهای مکانیکی، نیاز به آزمایشها و بررسیهای دقیق همیشه وجود دارد. این آزمایشها که با هدف بهبود عملکرد و کارایی سیستمها صورت میگیرند، معمولاً پرهزینه و زمانبر هستند و میتوانند باعث تأخیر در توسعهی محصول و افزایش هزینهها شوند. برای غلبه بر این چالشها و کاهش هزینهها، مهندسان و محققان به سمت شبیهسازی کامپیوتری روی آوردهاند. شبیهسازی به آنها این امکان را میدهد که قبل از ساخت واقعی، نحوه عملکرد سیستم را پیشبینی و بررسی کنند و مشکلات احتمالی را پیش از تولید کشف و رفع کنند.
یکی از رایجترین کاربردهای شبیهسازی، درک و تجزیه و تحلیل جریان سیالات است. دینامیک سیالات محاسباتی یا CFD (Computational Fluid Dynamics) شاخهای از مهندسی است که با استفاده از محاسبات عددی، رفتار سیال را شبیهسازی و پیشبینی میکند. CFD به مهندسان کمک میکند تا بتوانند ساختار و رفتار جریانهای سیال را در سیستمهای مختلف مانند موتورها، توربینها، سیستمهای تهویه و حتی سیستمهای زیستمحیطی شبیهسازی و تحلیل کنند.
درک معادله burger
معادله burger چیست؟
معادله برگر (Burgers’ Equation) یک معادله دیفرانسیل جزئی است که بهطور گسترده در دینامیک سیالات و ریاضیات کاربردی استفاده میشود. این معادله برای توصیف حرکت سیالات در شرایط مختلف کاربرد دارد و به دلیل سادگی نسبی خود، یکی از مدلهای رایج در آموزش و پژوهش در زمینه دینامیک سیالات به شمار میرود. این معادله میتواند به شکل خطی یا غیرخطی نوشته شود که فرم غیرخطی آن رفتارهای پیچیدهای مانند تشکیل امواج شوک و انتشار امواج را بهخوبی نشان میدهد.
اهمیت حل معادله burger
حل معادله برگر اهمیت زیادی در درک رفتارهای پیچیده سیالات مانند شوکها و آشفتگیها دارد. از آنجا که این معادله یک مدل سادهشده از معادلات پیچیدهتر است، به محققان و مهندسان این امکان را میدهد که روشهای عددی کارآمدی برای حل مسائل دینامیک سیالات پیچیدهتر توسعه دهند. همچنین، راهحلهای معادله برگر برای کاربردهای عملی متعددی از جمله مهندسی، هواشناسی و مطالعات زیستمحیطی نیز مفید هستند و به تحلیل دقیقتر و کارآمدتر رفتار سیالات کمک میکنند.
روشهای عددی برای حل معادله burger
دینامیک سیالات محاسباتی (CFD)
CFD یک روش محاسباتی برای تجزیه و تحلیل جریان سیال است که با استفاده از الگوریتمهای عددی، معادلات حرکت سیال را گسستهسازی و شبیهسازی میکند. این روش بهویژه در پروژههای مهندسی که نیاز به درک و پیشبینی رفتارهای پیچیده جریان سیال دارند، بسیار کاربرد دارد. با پیشرفت توان محاسباتی کامپیوترها، CFD به ابزاری بسیار مؤثر و محبوب در بین مهندسان و محققان تبدیل شده است.
مرور کلی بر روشهای عددی
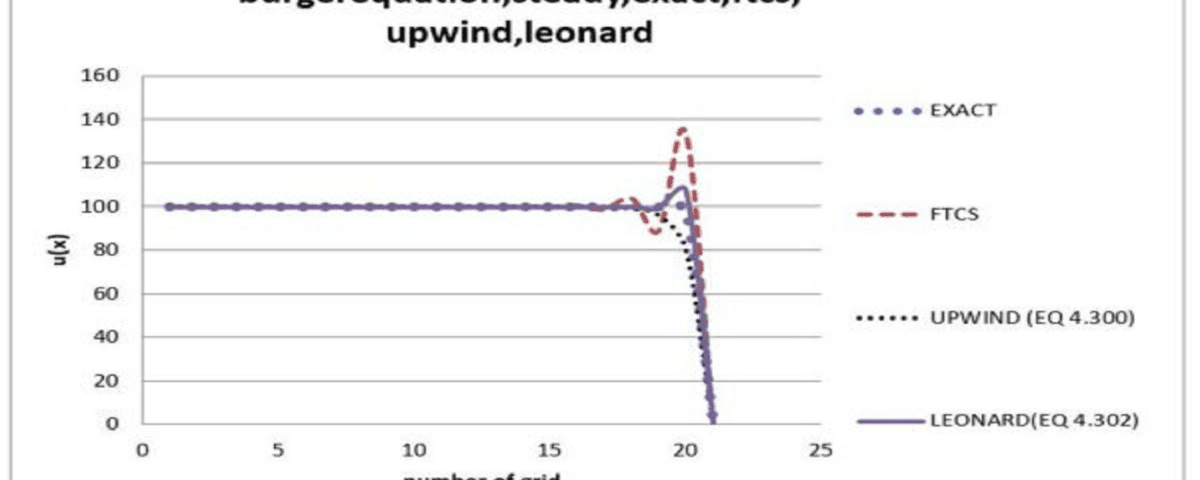
برای حل معادله برگر در این پروژه از سه روش عددی رایج استفاده شده است:
- روش FTCS (فضا-زمان متمرکز به جلو): این روش با استفاده از گسستهسازی زمانی و فضایی، معادله دیفرانسیل را به شکل یک معادله جبری تبدیل میکند که میتوان آن را بهصورت تکراری حل کرد. این روش برای حل معادلات خطی مناسب است و پیادهسازی آن ساده و قابل درک است.
- روش Upwind: این روش برای حل مسائل غالب جابجایی (Advection-dominated) مناسب است. روش Upwind با استفاده از اطلاعات از جهت بالادست، اثرات پراکندگی عددی را کاهش میدهد و پایداری بهتری نسبت به روشهای سادهتر برای حل مسائل غیرخطی مانند معادله برگر فراهم میکند.
- روش Leonard: این روش ترکیبی از روشهای FTCS و Upwind است و بهعنوان یک تکنیک پیشرفتهتر شناخته میشود. هدف این روش افزایش دقت در عین حفظ پایداری است، که آن را برای حل معادلات غیرخطی مانند معادله برگر مناسب میسازد.
پیادهسازی پروژه در فرترن
راهاندازی پروژه و انتخاب فرترن
زبان برنامهنویسی فرترن برای پیادهسازی این پروژه انتخاب شده است. فرترن به دلیل کارایی بالایی که در محاسبات عددی و شبیهسازیهای علمی دارد، انتخابی مناسب برای این نوع پروژهها به حساب میآید. این زبان بهویژه در محاسبات سنگین و پیچیده دینامیک سیالات کارآمد است و زمان محاسبات را به حداقل میرساند.
گسستهسازی معادله برگر
اولین گام در پیادهسازی، گسستهسازی معادله برگر با استفاده از روشهای عددی انتخابشده است. این فرایند شامل تبدیل معادله دیفرانسیل به معادلات جبری است که میتوانند بهصورت تکراری در طول زمان و مختصات فضایی حل شوند. این گسستهسازی برای شبیهسازی دقیق و پایدار میدانهای جریان سیال ضروری است.
تنظیم شرایط اولیه و مرزی
برای حل دقیق معادله برگر، تعریف شرایط اولیه و مرزی از اهمیت زیادی برخوردار است. شرایط اولیه مقادیر سرعت و فشار سیال را در شروع شبیهسازی تعیین میکنند و شرایط مرزی رفتار سیال را در لبههای دامنه شبیهسازی مشخص میکنند. تعریف صحیح و دقیق این شرایط تأثیر مستقیمی بر دقت و پایداری نتایج شبیهسازی دارد.
پیادهسازی الگوریتمهای عددی
الگوریتمهای اصلی هر روش عددی در فرترن پیادهسازی شدهاند. این الگوریتمها مسئولیت انجام محاسبات گامهای زمانی و گسستهسازی فضایی را برعهده دارند. هدف از این پیادهسازیها، دستیابی به راهحلهای دقیق و بهینه برای هر یک از روشها در شرایط مختلف است.
تحلیل نتایج و مقایسهها
پس از اجرای شبیهسازی، نتایج بهدستآمده از هر روش عددی با راهحل دقیق معادله برگر مقایسه میشوند. این مقایسه به ارزیابی دقت و کارایی هر یک از روشها کمک میکند و اطلاعات مفیدی در مورد نقاط قوت و ضعف هر روش ارائه میدهد.
اهداف پروژه
هدف از این پروژه، حل معادله برگر در حالت پایدار با استفاده از روشهای مختلف CFD از جمله روشهای FTCS (فضا-زمان متمرکز به جلو)، Upwind و Leonard و مقایسهی نتایج حاصل از آنها با حل دقیق است. پیادهسازی این پروژه با زبان برنامهنویسی فرترن انجام شده و کد منبع همراه با نتایج شبیهسازی موجود می باشد.