Introduction
The Blasius equation is a nonlinear ordinary differential equation used to describe the flow of a viscous, incompressible fluid over a flat plate under laminar flow conditions. Essentially, it’s a simplified form of the Navier-Stokes equations tailored for boundary layer flow.
What is a Boundary Layer?
When a fluid flows over a solid surface, the fluid velocity near the surface decreases due to friction. The region of the fluid where the velocity changes significantly due to these viscous forces is called the boundary layer.
Importance of the Blasius Equation
- Better understanding of fluid flow: The Blasius equation helps engineers and scientists better understand the behavior of fluid flow near solid surfaces.
- Design of hydraulic systems: It is widely used in the design of hydraulic systems, aircraft, ships, and other systems involving fluid flow.
- Calculation of friction factor: Solving the Blasius equation allows for the calculation of the friction factor between the fluid and the surface, which is crucial for calculating pressure drop in pipes.
- Foundation for many flow analyses: The Blasius equation serves as a fundamental equation in many fluid flow analyses, and many more complex equations are derived from it.
General form of the Blasius Equation
The Blasius equation is written as follows:
F”’ + FF” = 0
where:
- f is a dimensionless function of the similarity variable η.
- η is a similarity variable that represents the distance from the surface in terms of the boundary layer thickness.
Methods for solving the Blasius equation Due to its nonlinearity, the Blasius equation cannot be solved analytically. Therefore, numerical methods are employed. Some common methods for solving this equation include:
- Finite difference methods: In this method, derivatives in the equation are replaced by finite differences, transforming the equation into a system of algebraic equations.
- Finite volume methods: This method is widely used for solving partial differential equations in engineering fluid mechanics.
- Finite element methods: This method is well-suited for solving partial differential equations in complex geometries.
Applications of the Blasius Equation
- Meteorology: For predicting wind movement near the ground
- Aerospace: For designing aircraft wings and reducing drag
- Naval engineering: For designing ship hulls and reducing drag
- Oil and gas industry: For designing pipes and fluid transfer equipment
In conclusion, the Blasius equation is a powerful tool for analyzing fluid flow in boundary layers and has numerous applications in various engineering fields.
Would you like to Delve Deeper into a Specific Aspect of the Blasius Equation?
For example, we could discuss:
- Numerical solutions to the Blasius equation
- Specific applications of the Blasius equation
- Comparison of the Blasius equation with other boundary layer equations
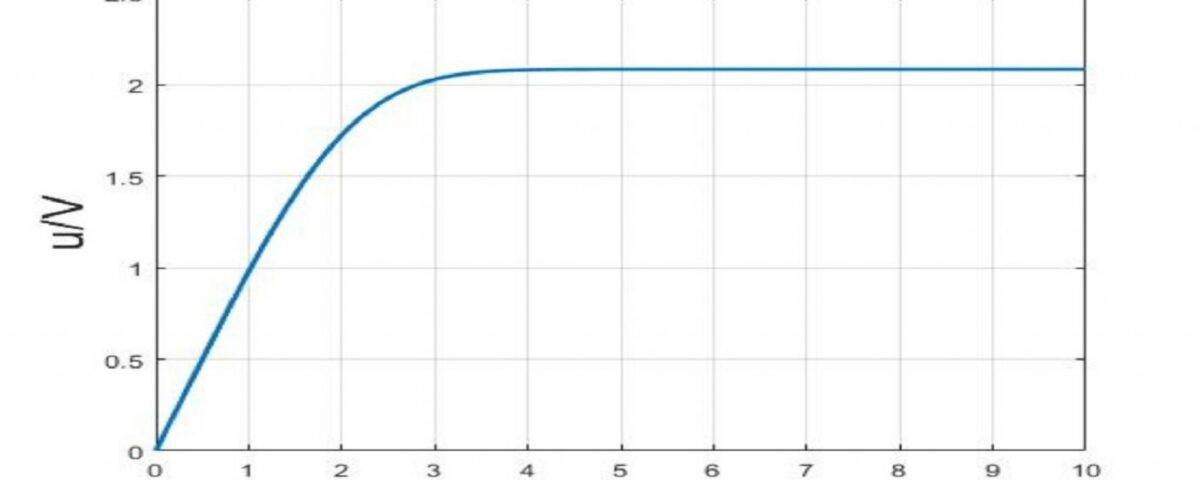
This project demonstrates the simulation of external flow over a flat plate using the Blasius method in MATLAB. The focus is on steady-state, laminar flow over a flat plate and its numerical solution using the Blasius equation. Initially, the continuity and momentum equations are non-dimensionalized based on boundary layer assumptions. Subsequently, the domain is discretized for an explicit solution of these equations. Finally, the results, including velocity vectors, velocity contours, streamlines, and vorticity contours, are visualized.
The MATLAB code implements the Blasius equation for steady laminar flow over a flat plate using the shooting method and a fourth-order Runge-Kutta scheme. The entire code comprises 38 lines.