Introduction
Membranes act as barriers that separate two solutions of different concentrations. and allow only certain substances, such as solvents, to pass through. while preventing the passage of other substances, such as solutes. These processes reach equilibrium based on specific mechanisms and different driving forces.
Membranes are divided into natural and synthetic categories. Natural membranes in the body of living organisms and artificial membranes are mainly made of polymers and are used in various industries. These membranes play a key role in various processes such as reverse osmosis, nanofiltration, ultrafiltration, microfiltration, electrodialysis, and permeation evaporation.
The main difference between these processes is in the mechanism of passing through the membrane and the type of driving force that makes each of them suitable for various applications. For example, in reverse osmosis, which is used to separate very small solutes such as ions. The driving force is the hydrostatic pressure difference that exceeds the osmotic pressure of the solution.
In addition to spatial hindrance or molecular sieve, the force of interaction between the polymeric material of the membrane and the solution is also effective in this process. In contrast, in ultrafiltration, which is used to separate larger substances such as proteins. The pressure difference is less and the separation mechanism is more based on spatial hindrance.
Membrane processes have significant advantages, including:
1. Simplicity in operation.
2. wide and varied application,
3. High flux and effective separation,
4. Maintaining the solution phase and reducing energy consumption, which is especially important in heat-sensitive materials such as food and medicine.
5. Operation at a constant temperature without the need for heating or cooling.
(RO): Process, Applications and Challenges
Reverse osmosis or (RO) is one of the most important water purification methods in which water flows from a dilute solution to a concentrated solution, using a semi-permeable membrane and applying external pressure. In the natural state (osmosis), water automatically moves from a less concentrated solution to a more concentrated solution. to create a balance. But in the process of reverse osmosis, by applying pressure, the flow of water is directed in the opposite direction.
In this process, saltwater or seawater is first compressed at high pressure (usually between 55 and 85 bar) to overcome the osmotic pressure. Pure water (permeate) passes through the membrane and is directed to the outlet. While solutes and salts soluble in water remain in the remaining part (retentite). This process can remove between 95 and 99% of salts and pollutants soluble in water.
Challenges of Using Reverse Osmosis
One of the main challenges of this technology is the high energy consumption to produce the necessary pressure. To reduce these costs, energy recovery devices such as energy recovery turbines (ERT) and pressure transducers (PX) are used. which can recover up to 50-60% of the required energy.
Polymeric Membranes: The Heart of The Reverse Osmosis Process
Membranes used in reverse osmosis are usually composed of polymeric materials. These membranes have a thin and active layer that creates the main resistance to the passage of salts. This thin layer is placed on a porous support layer that provides the mechanical strength necessary to withstand high pressures. These membranes are usually placed in parallel modules to provide sufficient surface area for water treatment.
Applications and Benefits of Reverse Osmosis
Reverse osmosis has wide applications due to its high efficiency in removing solutes and small ions. This technology is used in the production of drinking water, food, pharmaceutical and electronic industries. Also, in areas such as the Middle East and North Africa that are facing water shortages. This technology is widely used to supply fresh water. However, high energy costs and the need for initial investment are among the main challenges of this technology. Especially in countries with limited financial resources.
Mathematical Modeling and Optimization
Modified Surface Force-Pore Flow Model (MD-SF-PF)
The SF-PF model, which was developed by Mehdizadeh and Dixon, was not able to correctly explain the experimental data. These defects were mainly caused by incorrect use of the mass balance equation and neglecting the effect of osmotic pressure. For this reason, the MD-SF-PF model was introduced as an improved version that fixed the shortcomings of the previous model and its equations were significantly different from the original model.
The MD-SF-PF model is based on fundamental modifications of the mass and velocity balance equations. Specifically, the concentration distribution of the dissolved substance is obtained from the mass balance equation as follows.
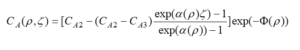
The velocity distribution is calculated by the momentum balance equation.
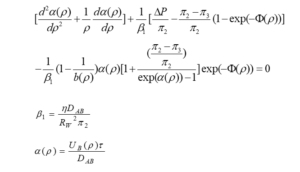
The new potential function in the MD-SF-PF model is introduced as follows. This function, in contrast to the SF-PF model, correctly considers the effects of geometry and osmotic pressure.
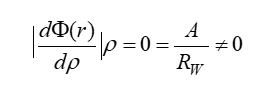
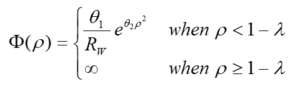
To describe the hydrodynamic drag, the MD-SF-PF model uses the modified friction function. This function changes radially.
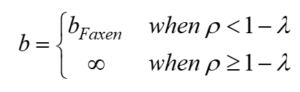
Modified Generalized Model of Surface Force-Pore Flow (Ex-MD-SF-PF)
The modified generalized model of surface force-pore flow (Ex-MD-SF-PF) offers improvements over the previous model (MD-SF-PF) and has differences in the calculations and equations used.
In the radial component of the dissolved substance flux, assuming balance in the radial direction, the flux equation is expressed as follows (Boltzmann distribution equation):
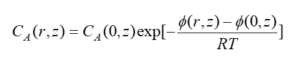
In the axial component of the dissolved substance flux, the total driving force for the dissolved substance is obtained from the change of the chemical potential and the equation of the dissolved substance flux in the axial direction as follows:
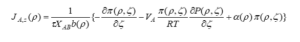
To determine the velocity distribution, the differential equation of velocity inside the cavity with force balance is as follows:
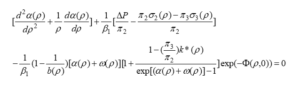
Separation and membrane fluxes are also calculated based on the following relations:
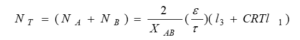
In the Ex-MD-SF-PF model, the potential function has been updated and is now a function of the radial, axial direction and the concentration of the resolved substance:
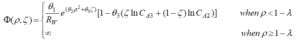
The friction function in this model is improved compared to the previous model and is considered as a function of the radial direction:

Optimized Equations and Functions
These modifications in the MD-SF-PF model have significantly improved the performance predictions of reverse osmosis membranes and more accuracy compared to the SF-PF and Ex-MD-SF-PF models. In the following, the results of the modified models and their optimization will be reviewed.
Development of New Functions in Reverse Osmosis Membrane Models
In order to obtain new potential and friction functions in reverse osmosis models, there must be certain criteria for choosing the best proposed form of the equations. These criteria are chosen with the aim of more accurately predicting the performance of reverse osmosis membranes based on laboratory data.
The optimization process allows us to identify the optimal functions among several proposed functions using the guess and error method. Before entering into the optimization details, explanations about the potential and friction functions and the necessity of their development are provided.
Potential Function and Friction in Porous Membranes
The potential function represents the interaction between the membrane and the solute and describes the forces acting on the solute by the walls of the membrane cavity. The size of this function depends on various factors such as the material of the membrane wall, the type of dissolved substance and the system conditions such as concentration and temperature. On the other hand, the friction function is used to describe the hydrodynamic drag applied to the solute by the cavity walls. And it plays an important role in different models of porous membranes.
The Reason for The Development of New Functions
1. In the MD-SF-PF model, the potential function is considered only one-dimensional and as a function of the radial direction inside the cavities. But the proposed new functions are not only a function of the radial and axial direction, but also have a special dependence on the concentration of the dissolved substance.
2. In the MD-SF-PF model, the constant friction function is calculated based on Faxen’s equation. On the contrary, the new functions have a radial dependence that better matches the reality governing the system.
3. Although in the Ex-MD-SF-PF model, the friction function depends on the radius, but the proposed form of this function is old and related to 1985. The new functions are not only more up-to-date, but also more in line with the true nature of the system.
Optimization and Criteria for Choosing Optimal Functions
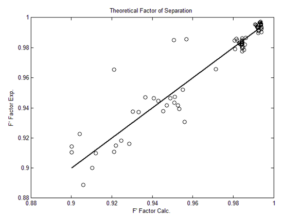
The optimization process is such that after guessing the desired function, parameters such as separation factor, total flux and pure solvent flux are calculated for each model. Then by defining an objective function, the value of this function should reach the minimum possible value. The objective function proposed in this research is more accurate than the previous models because it includes all key performance parameters of membranes.
Coefficients of the above equation have been selected using the guess and error method.
Objective function used by Mehdizadeh and his colleagues in the Ex-MD-SF-PF model is as follows:
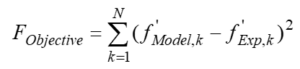
Finally, in order to evaluate the accuracy of the models, the “RMSD” parameter is used. The closer the value of this parameter is to zero, the more suitable the selected model is.

In this regard, OF is the numerical value of the objective function, the number of optimized parameters and the number of experimental data. This optimization method has provided reliable results by examining all possible states for the potential and friction functions.
In order to simplify and avoid repeating relations, the potential function of the Ex-MD-SF-PF model, which was previously expressed in the following equation, is displayed. Other suggested functions are shown below according to the following equations:
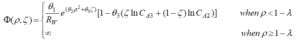
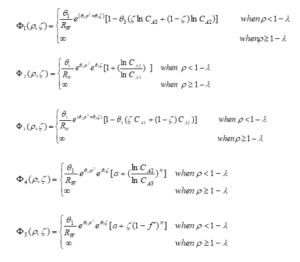
The same has been done for the friction function. The friction function of the Ex-MD-SF-PF model presented earlier, and other proposed functions are displayed as follows:


Considering that (5) the potential function and (4) the friction function are available, for a general and comprehensive review, all possible states have been examined and the results of which include (20) states have been examined in this project.
Conclusion
In this research, the differential equations of two MD-SF-PF and Ex-MD-SF-PF models were solved using finite difference and finite volume numerical methods. The velocity equation was solved by the finite difference method and the concentration equation was solved by the finite volume method. The results obtained from these methods showed high accuracy and were simpler and more efficient, especially compared to orthogonal interpolation numerical methods used to solve similar models.
In the following, new potential and friction functions were introduced and optimized. Using the guess and error method, various functions were selected and optimized for the Ex-MD-SF-PF model in order to identify suitable functions and parameters. The proposed new model, named “New-Ex-MD-SF-PF”, showed the best performance by examining the objective function and the rmsd parameter.
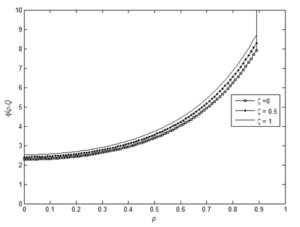
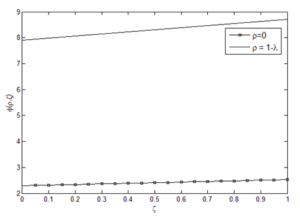
Membrane performance for “New-Ex-MD-SF-PF” and “Ex-MD-SF-PF” models was compared graphically and numerically.
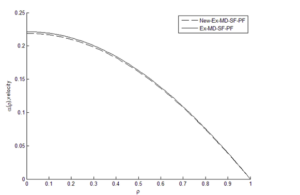
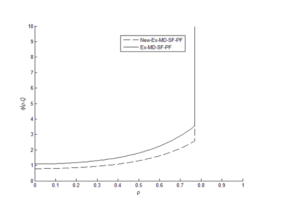
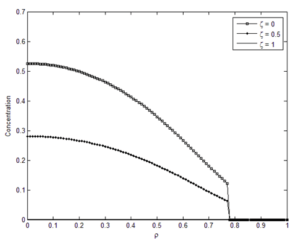
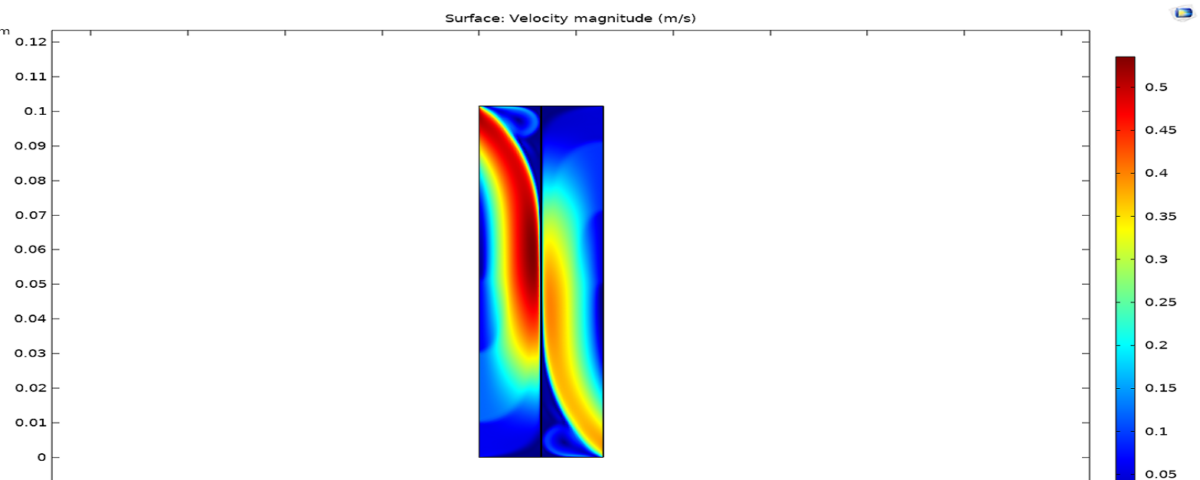
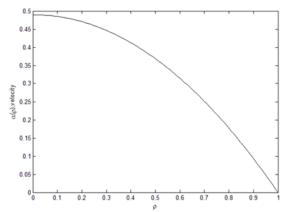
The results showed that the “New-Ex-MD-SF-PF” model is more accurate in predicting membrane performance. Distribution of concentration and velocity and change trend of the potential function were investigated for both models. Concentration changes are such that a greater amount is observed at the beginning of the cavity than at the end of cavity. And “New-Ex-MD-SF-PF” model shows a lower concentration drop at the end. The velocity distribution is also slightly different between two models and reaches zero near the cavity wall.
Finally, the effect of the potential function on the results of the “Ex-MD-SF-PF” model was investigated and it was found that the “Ex-P4-F1” model with the new potential function provides the best results. The prediction graphs of the membrane performance for this model confirmed that the change trend of velocity distribution and potential function is similar to the original model.
Simulation With Comsol
The simulations performed with Comsol software and based on the data of the article, have analyzed the performance of reverse osmosis membranes in detail. These simulations are specifically designed to investigate key changes such as temperature, concentration, and flux, etc. within reverse osmosis systems. The purpose of these simulations was to improve our understanding of the effect of these parameters on the overall performance of membranes and their associated processes.
To achieve this goal, optimized equation models, which include “New-Ex-MD-SF-PF” models. have been used as a basis for these analyzes and have guaranteed the accuracy of the simulation results.
Model Definition and Simulation Components
The exact geometry and physical and chemical properties of the materials are defined according to the optimized equation models. These definitions are used in order to increase the accuracy of simulations and match them with real conditions. Boundary and initial conditions are also set using these models so that the simulation results are more accurately close to reality.
Using the optimized equations, the simulations have analyzed the heat and mass transfer in reverse osmosis membranes in detail. The results of these simulations, including changes in temperature and concentration, have been analyzed with the help of contour maps and diagrams. These analyzes are based on “New-Ex-MD-SF-PF” models and have helped to identify distribution patterns and different regions of temperature and concentration. Finally, the optimized model “New-Ex-MD-SF-PF” which explained earlier, to.
The main basis of analysis and simulation results have been used. This model, with updated corrections and detailed optimizations, has provided the ability to predict the performance of reverse osmosis membranes better than the previous models. Using this model in simulations has significantly increased the accuracy and efficiency of analyzes and made the obtained results more reliable.
Analysis of The Results
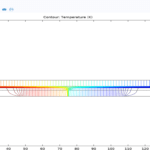
1. Temperature changes: To investigate the effects of temperature on membrane performance, temperature changes inside the membrane have been analyzed in the form of graphs and contours. This investigation has helped to identify hot and cold spots along the membrane. and the effects of temperature on heat transfer and separation are investigated. The results obtained from the simulation have shown that the temperature distribution inside the membrane significantly affects the efficiency of the reverse osmosis process.


2. Concentration distribution: The changes in concentration of pure water along the membrane have been analyzed with the help of the relevant contours. This analysis has contributed to a better understanding of how the solute is distributed and its effect on the separation process. In particular, the concentration distribution is carefully evaluated in comparison with optimized models such as “New-Ex-MD-SF-PF” and important differences in the performance of different models are simulated.
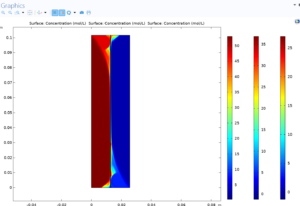
Heat flux: Analyzing the heat flux inside the membrane is very vital to investigate the distribution and transfer of thermal energy. Using heat flux diagrams, the temperature distribution and the amount of heat transfer inside the membrane have been investigated. This analysis helps to identify areas with temperature differences and analyze the effect of temperature changes on the overall performance of the reverse osmosis process.
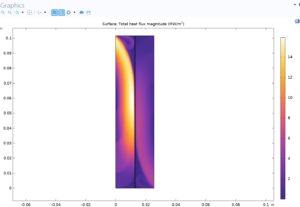
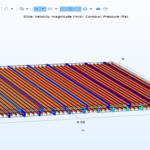
Flow: Analyzing the flow through the membrane is very important to evaluate the rate of material transfer and the effect of various parameters such as pressure and temperature on the flow. Flow diagrams show the distribution and flow intensity of materials within the system. This analysis helps to better understand how reverse osmosis systems work and improve their design and performance.
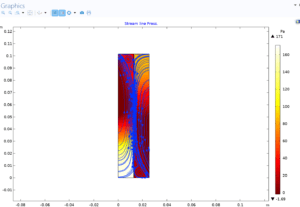
Conclusion
Simulation results with COMSOL software, which are obtained based on optimized equation models. They have contributed to a deeper understanding of the performance of reverse osmosis membranes and process optimization. Detailed analysis of temperature changes, concentration and heat flux and flow has led to determining the optimal operating conditions and improving the efficiency of the systems. These results have effectively contributed to the primary goals of research and optimization of the processes and systems used.
Modeling and Simulation of Reverse Osmosis Membranes Using Comsol
In this project, the modeling and simulation of reverse osmosis membranes has been done using Comsol software based on the article, in order to accurately evaluate the performance and characteristics of these membranes in water purification processes. This project comes with full training.