توضیحات
روشهای عددی مجموعهای از تکنیکهای محاسباتی هستند که برای حل مسائل ریاضی پیچیده، به خصوص معادلات دیفرانسیل و جبری که حل تحلیلی برای آنها وجود ندارد، به کار میروند. این روشها به ما اجازه میدهند تا با تقریبهای عددی به جوابهای دقیقتری برسیم.
متلب یک نرمافزار قدرتمند برای محاسبات عددی است که به دلیل سادگی استفاده و کتابخانههای گسترده، به طور گستردهای در مهندسی، علوم و سایر زمینهها مورد استفاده قرار میگیرد. یکی از کاربردهای مهم متلب، پیادهسازی روشهای عددی مختلف است.
روش نیوتن – رافسون
در آنالیز عددی روش نیوتن ، که همچنین به عنوان روش نیوتن-رافسون نیز شناخته میشود الگوریتم ریشه یابی است که تقریب های خوبی در نزدیکی ریشه یک تابع (صفرهای یک تابع) میزند.در پایه ای ترین حالت، الگوریتم نیوتن برای یک تابعی چون با متغیر و با مشتق به همراه حدس اولیه بکار میرود. اگر تابع حدس کافی و دقیقی را برآورد سازد و همچنین حدس اولیه نزدیک به ریشه تابع مفروض باشد (که با همگرایی تقریب ها این موضوع روشن می شود) آنگاه تقریب بهتری نسبت به به حساب می آید.چرا که با احتساب همگرایی جواب ها، هر تقریب نسبت به تقریب قبل از خودش از دقت بالاتری برخوردار بوده و به ریشه تابع نزدیک تر است.به لحاظ هندسینقطه ای است که محور و خط مماس تابع در نقطهٔ یکدیگر را قطع میکنند. شکل عمومی الگوریتم نیوتن به شرح زیر میباشد:
که در اصل از رابطه:
بدست امده است. میدانیم که در نقطهٔ برخورد تابع با محور مقدار تابع صفر خواهد بود لذا :
که در آخر با تقسیم بر میتوان رابطه را به فرم رو به رو بازنویسی کرد:
همانطور که مشهود است روش نیوتن-رافسون از سری تیلور ناقص تابع مفروض به عنوان یک تقریب خطی حول نقطهٔ حدس اولیه بهره میبرد و از این جهت تقریب را ناقص میگویند که نیازی به نوشتن سری تابع تا مراتب بالاتر نبوده و به همان دو جمله ابتدایی بسنده میکند که این موضوع نیز دلیلی بر تقریب خطی بودن روش نیوتن میباشد. همچنین چون این روش معادلهٔ یک تابع را تا معادلهٔ یک تابع درجه یک تقیل میدهد، لذا صرف نظر از اینکه تابع چند ریشه دارد، در نهایت الگوریتم تنها یک جواب بدست می آورد.
روش وتری
یکی از روشهای یافتن ریشه معادله است. علت نامگذاری این روش این است که در مرحله n نقطه n+1x از محل برخورد خط با نمودار بهدست میآید. مزایا و ویژگی این روش نسبت به روش نیوتن این ویژگی را دارد که به مشتق تابع نیازی ندارد. همچنین نسبت به روش نقطه ثابت، لازم نیست که دو نقطه حدس آغازین ما دو طرف ریشه تابع قرار داشتهباشد. این روش تضمین همگرایی ندارد. اما اگر همگرا باشد، به سرعت به ریشه نزدیک میشود.
روش تکرار نقطه ثابت
در بحث محاسبه غلظتهای تعادلی در واکنشهای تعادلی، همچنین خوب است با بحث حل معادلات با استفاده از روش های عددی آشنا باشیم. همانطور که تاکنون دیده ایم، در اغلب موارد برای بدست آوردن غلظتهای تعادلی نیازمند حل معادلات و بدست آوردن مجهولات درنظر گرفته شده هستیم. برای حل معادلات بطور کلی دو دسته روش درنظر گرفته میشود: روشهای تحلیلی و روشهای عددی یا معادلاً روشهای مستقیم (Direct Methods) و روشهای تکرار شونده (Iterative Methods).
روشهای مستقیم جواب دقیق یک معادله را براساس یک الگوریتم معین و با طی تعدادی مراحل مشخص نتیجه میدهند. بعنوان مثال روش دلتا یک روش مستقیم برای یافتن جوابها یا ریشههای معادلات درجه دو است. متأسفانه برای حل بسیاری از معادلات روشهای مستقیم وجود ندارد و ما برای حل اغلب معادلات مجبوریم به روشهای تکرار شونده یا عددی متوسل شویم. روش های عددی متنوعی وجود دارند و بسیاری از نرم افزارها در کامپیوترها یا ماشین حسابها از این روش ها به یافتن جواب استفاده می کنند. در اینجا ما یک روش عددی برای حل معادلات به نام تکرار نقطه ثابت (Fixed-point Iteration) در نرم افزار متلب را ارائه میدهیم.
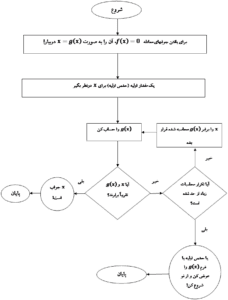
کد متلب روش های عددی زیر موجود می باشد:
- False Position
- Bi Section
- Fixed Point
- Newton-Rophson
- Modified Newton-Rophson
- Vatari